Today I woke up with the intention of messing it up, I’m going to increase the entropy to mess my the place where I work a little bit and I’m going to send one of those e-mails that… wait a moment, entropy? What does that mean? Stop inventing words leave it to philologists!
Actually I’m not inventing any word, although I may be using it incorrectly, but let’s start from the beginning, just in case the entropy increases even more 🙂
In our day-to-day life, we are used to find situations that happen in a specific direction and not in the opposite one. When an egg falls down the table, we see it breaks and have to clean the floor. We never see how the egg, recomposes itself and goes up again to the table, what would be great to avoid cleaning the floor. This is a classical example (I always wanted to use it as an example) but there are many more, such as when we open a soft-drink and the gas escapes the tin, when we put an ice cube in a glass of water and it melts or when a computer with Windows operative system shows a message like ‘an unexpected error occurred and the software will close’, it never opens itself again and may happen that you need to buy a new computer with a more reliable operative system.
All these processes are denominated irreversible processes, that mean that they only progress in one direction, or in other words, they evolve only in one direction.
In the middle of the XIX century, Rudolf Julius Emmanuel Clausius, better known as Clausius by those who suffer it during the Thermodynamics courses, tried to find a measure to quantify the trend of any system to make a specific change and that verified the direction in which the change was taking place. Because he was German, he introduced the Greek word ετυροπη that means evolution and that has been transmitted to us as entropy and it is represented by the letter S. Entropy, as a physical measurement, measures the capability to make a change as Clausius intended. It is an intrinsic property of matter and its value depends only on the nature of the body considered and its state.
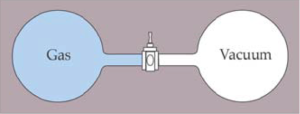
Let’s consider a simpler example than the egg that falls, and to do that we will consider a classical experiment known as Joule’s experiment or free expansion.
In this experiment Joule, introduced a gas in a container linked to another one where a vacuum had been made. The complete system is isolated from the outside world so that it cannot exchange any type of energy in the form of heat. A valve that is initially closed separates both containers. When the valve is opened the gas expands freely towards the container where the vacuum is made until it fills the complete volume of the two containers. If we wait until the gas completely returns to the initial container while the other ones is completely empty, we will probably lose our time and will get old because the process is irreversible. What has happened? The obvious aspect is that the gas that initially was filling a small volume V1 is now filling a bigger volume V2. If we calculated (mathematically) the entropy of the system comprising both volumes plus the outside world (remember that the system is isolated and does not exchange energy in the form of heat) we would see that by subtracting the initial entropy from the final one, this difference is greater than zero, or in other words, the entropy has increased.
The same happens with the case of the egg that falls to the floor, the entropy of the universe (understood as the egg plus the table plus the floor plus the air between the table and the floor) increases.
At this point where I have not written any mathematical formula yet, I think that the concept of entropy is not clear yet. And it is an issue because entropy is one of the scientific ideas that have been more difficult to understand by students and by most of the professors that tried to explain it, so if you have understood the concept, please explain it to me!
Let’s now turn it everything upside down. Up to now we have been in a macroscopic world, but now we enter into the craft from the Innerspace film to go to the microscopic world to see if we understand it a little bit more. Once we are miniaturized to the size of a gas molecule, we enter the container that is filled with the gas of the Joule’s experiment and wait until the valve is opened. While we are waiting, as we are bored, we count the number of gas molecules in the container and we see, because the container is very small and the gas is expensive, that Joule has only been able to buy 10 molecules. Now the valve is opened. What is what we see? We start seeing that one molecule shifts to the other container, then another one shifts too, after it we move and the rests of molecules follow us except for one. Once we are in the other container another molecule flows back to the initial container suddenly, then another one, then another one, and finally all of them flow back except for us, who are left alone. But the situation does not last for a long time because a moment later three molecules are coming back to be with us until one of the decides to go again to the initial container… I could keep going on and on but I’m getting tired of writing, so you can imagine how it continues.
What has happened here? We have said that the Joule’s experiment gave an idea of irreversibility of the process, but at a microscopic scale we have been very close to a reversible process, or in other words that all the molecules were back in the initial container (only we remained). How is it possible? At a microscopic level there are many things happening that we cannot see and that scape our intuition. At the microscopic level, there is a probability that all the particles are in the same state, which is smaller as the particle number increases, in other words, the number of possible states increases (to understand it a bit, and although it is NOT totally correct, let’s assimilate the concept of state as the location of the molecule in one or other container). As long as the number of possible states increases, it also increases the disorder of the system. Because any molecule is in a different state, it will be doing whatever it wants increasing the disorder of the system. The entropy, at a microscopic level, depends of this number of possible states, therefore the larger the number of states, the larger the entropy. But as we said, the larger the number of states, the greater the disorder and therefore we conclude that the entropy is a measure of the disorder of the system. Although the word entropy is derived from the Greek word evolution, I was using it correctly at the beginning because it has to do with disorder, so If I send the e-mail I have in mind, I’m going to turn it all upside down!
References
Paul A. Tipler. Física. Editorial Reverte.
José Aguilar Peris. Curso de Termodinámica. Alhambra Longman